ECE 291 - Electrical Engineering Laboratory
LAB 7: INPUT IMPEDANCE OF AN OSCILLOSCOPE AND THE SCOPE PROBE
OBJECTIVES
Measurement of the oscilloscope input impedance. Principles of operation and usage of the scope probe.
INTRODUCTION
After becoming familiar with the frequency response of RC circuits in the previous laboratory, you are ready to learn about the oscilloscope input impedance. This complex impedance, which has resistive and capacitive components, can disturb performance of circuits being measured and limits high frequency performance of oscilloscopes. The current flowing through the capacitive load depends on frequency, and this can make measurements with the scope depend on frequency. Fortunately there is a remedy, which you should know about: the scope probe.
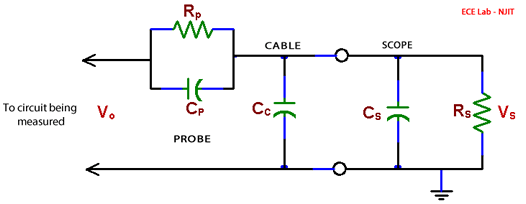
RS -scope internal resistance, CS scope internal capacitance,
CC - cable capacitance, RP - probe resistance, CP - probe capacitance
A scope probe is essentially a 10:1 attenuator with a resistor and a capacitor at the end of the probe cable. The attenuator consists of two impedances in series, one of which is the scope’s own impedance to ground while the other is attached between the point of measurement in a circuit and the scope input (see Fig. 5). The scope internal impedance has a capacitive component Cs. Note, however, that the capacitance of the scope cable (Cc) sums with the internal capacitance of the scope input. This not only increases the capacitive load (Cs + Cc) on the circuit being measured but also makes this load dependent on the length of the cable used, especially that usually Cc > Cs. The scope probe solves this problem not by eliminating these capacitances (which is not possible) but by compensating it with another capacitance. The probe capacitance (Cp), connected in series with the scope, can be adjusted so that the measurement is independent of frequency. To understand how this works, consider the voltage seen by the scope (Vs), if the voltage to be measured is Vo. From the voltage divider formula:
![]()
where Z1 is the scope impedance (including the cable capacitance CC), so that Z1 = RS ||CS || CC or
![]()
where C = Cs + Cc.
Z2 is the probe impedance, Z2 = Rp||Cp or
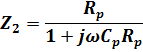
If we make ![]() a real number then the relationship
a real number then the relationship ![Vs = [Z1/(Z1 + Z2)]Vo](images/291-7-2.gif) will not depend on the frequency and there will be no phase difference between Vs and Vo. By using the expressions for Z1 and Z2, given above, you can easily check that this condition will be satisfied when Rp Cp = Rs C. Since Rsand C is specified by the scope and the cable, designing the probe we can chose appropriate Rp and Cp. We also want to minimize the capacitive load on the circuit so we chose Cp < C . Typical 10:1 probe has Cp = C/9 and therefore Rp = 9 Rs. This decreases 10 times the instrument capacitive load on a circuit at the expense of attenuating the amplitude by the same factor; a fair trade for high frequency measurements. There are also 100:1 scope probes.
will not depend on the frequency and there will be no phase difference between Vs and Vo. By using the expressions for Z1 and Z2, given above, you can easily check that this condition will be satisfied when Rp Cp = Rs C. Since Rsand C is specified by the scope and the cable, designing the probe we can chose appropriate Rp and Cp. We also want to minimize the capacitive load on the circuit so we chose Cp < C . Typical 10:1 probe has Cp = C/9 and therefore Rp = 9 Rs. This decreases 10 times the instrument capacitive load on a circuit at the expense of attenuating the amplitude by the same factor; a fair trade for high frequency measurements. There are also 100:1 scope probes.
If the probe impedance is not matched properly to the scope internal impedance, the system acts like a filter and the attenuation depends on frequency. Fortunately there is an easy way to adjust the probe impedance since Cp is a small trimming capacitor while Rs is kept constant. A filter distorts a square wave so the trimming capacitor can be adjusted by observing a distortion of a square wave on the scope screen. Oscilloscopes are equipped with an internal square wave generator for easy probe adjustments. The probe test terminal is provided on the scope front panel. The probe capacitor is adjusted until there is no distortion of the square wave.
A scope probe is a very handy device used by professionals all the time. From now on you should use it too!
Measuring the impedance of an oscilloscope
Measuring the scope internal resistance (RS) is easy; just like a voltmeter resistance, using a DC source. For measurements of the scope internal capacitance AC source must be used, of course. An external resistor R is put in series with the voltage source (instead of the probe in Fig. 5).
From the voltage divider formula: ![Vs = [Z1/(Z1 + Z2)]Vo](images/291-7-2.gif) where Z1 is the scope impedance (including the cable capacitance Cc), so that Z1 = Rs||Cs||Cc or
where Z1 is the scope impedance (including the cable capacitance Cc), so that Z1 = Rs||Cs||Cc or ![]() where C = Cs + Cc.
where C = Cs + Cc.
Z2 is just the external resistance R, Z2 = R
Measuring amplitudes Vo, Vs of Vo and Vs gives us:
where red letters denote complex variabl![]() es while a and b are the real and the
imaginary parts of the impedance ratio in the last equation.
es while a and b are the real and the
imaginary parts of the impedance ratio in the last equation.
PRELAB
If the scope internal resistance RS = 1 MΩ, its capacitance is CS = 25 pF and the cable connecting the probe to the scope has capacitance CC = 150 pF, find the values of the required probe resistance RP and capacitance CP for 10:1 attenuation. Make sure that the same attenuation is also valid for dc measurements.
Hint: Consider independently two voltage dividers, one resistive the other capacitive. Note that they are connected in parallel and should give the same attenuation.
LABORATORY
Equipment needed from the stockroom: scope probe, resistance substitution box, proto-board, leads.
1. MEASUREMENT OF THE INTERNAL IMPEDANCE OF AN OSCILLOSCOPE.
The input impedance of an oscilloscope is a complex quantity which can be represented by a resistance in parallel with a capacitance between the scope input terminal and the ground. The impedance is thus frequency dependent.
a) First, determine the internal scope resistance with a DC signal. Apply the same method as used for the measurement of a voltmeter internal resistance. You may use a resistance substitution box for this measurement. Select resistance which causes the voltage to drop to about 1/2 of the voltage measured directly (without the resistance).
b) Repeat the measurement but instead of DC use a sinewave signal with a frequency at which the scope impedance is significantly different from the measurement a). Since the AC scope impedance is lower than its DC impedance (because of the parallel capacitance), use a resistor of a smaller value than in a). Moreover, the voltage measured by the scope depends now also on frequency, because the ratio of the voltage divider formed by the external resistor and the scope impedance depends on frequency. A resistor of a few tens of kilo ohms and a frequency of a few tens of kilo hertz is a good choice. Do not use resistance substitution box in this case as its capacitance may influence the measurement.
c) Using a capacitance meter available in the laboratory, measure the capacitance of the coaxial cable connected to the scope during these measurements. The cable capacitance contributes to the scope capacitance seen by the circuit. Determine also the cable length and calculate its capacitance per unit length.
2. SCOPE PROBE.
2.1. Check your scope probe by connecting it to the probe calibration terminal on your scope (a small tab usually with a hole on the front panel). Properly adjusted probe should give the same attenuation for all frequencies, which means that it passes a square wave signal without distortion. If you do not see a perfect square wave, using a small screwdriver adjust the probe trimming capacitor which tunes Cp.
2.2. To see the benefits of using the probe make a 2:1 resistive voltage divider, using equal resistors of 50 k to 100k. Particular resistance values are not critical, as long as you know their ratio; check it with the digital ohmmeter. Measure attenuation of a sinewave at two frequencies, in 10 kHz and 100 kHz range using (a) scope without the probe (b) scope with probe.
3. CIRCUIT SIMULATION (at home).
Simulate the circuit representing an oscilloscope probe (Fig. 5). Use the values of RS, CS, and CC, from your measurements and the corresponding values of RP and Cp for 1:10 attenuation.
a) Simulate the effect of tuning of CP (by slightly increasing and decreasing it from the "ideal" value) on the shape of a square wave at the probe input. Compare also frequency responses of a tuned and an out of tune probe.
b) Simulate the measurements 2.2 with and without the probe.
REPORT
- Calculate RS from dc the measurement in 1. With the known value
of RS and the ac measurements in 1, calculate Cs (see
the introduction to this laboratory). Do not forget to subtract the cable
capacitance. RS and CS determine the input impedance
of the scope.
- Explain the result of measurements in 2.2.
- The fact that the scope probe attenuates the signal does not appear to be an advantage. Why then is the probe so useful in scope measurements?