Experiment 3: Systolic-Array Implementation of Matrix-By-Matrix Multiplication
Review the help notes for this experiment.
Objectives
The multiplication of matrices is a very common operation in engineering and scientific problems. The sequential implementation of this operation is very time consuming for large matrices; the brute-force solution results in computation time O(n3), for n x n matrices. For this reason, several parallel algorithms have been developed to solve this problem more efficiently. Here, a simple parallel algorithm is presented for this problem and a "hardwired" (actually, systolic-array) implementation of the algorithm becomes our objective.
Introduction
2-dimensional, mesh-connected parallel computers are often used in systolic-array configuration for the multiplication of matrices. For the sake of simplicity, we assume input matrices of size 4 x 4 containing one-bit integer elements. Figure 3.1 shows the operations to be performed. The ● and + represent the integer operations multiplication and addition, respectively.
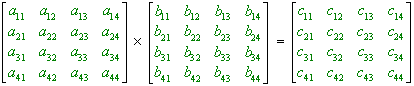
c12 = a11 ● b12 + a12 ● b22 + a13 ● b32 + a14 ● b42
c13 = a11 ● b13 + a12 ● b23 + a13 ● b33 + a14 ● b43
c14 = a11 ● b14 + a12 ● b24 + a13 ● b34 + a14 ● b44
c21 = a21 ● b11 + a22 ● b21 + a23 ● b31 + a24 ● b41
c22 = a21 ● b12 + a22 ● b22 + a23 ● b32 + a24 ● b42
c23 = a21 ● b13 + a22 ● b23 + a23 ● b33 + a24 ● b43
c24 = a21 ● b14 + a22 ● b24 + a23 ● b34 + a24 ● b44
c31 = a31 ● b11 + a32 ● b21 + a33 ● b31 + a34 ● b41
c32 = a31 ● b12 + a32 ● b22 + a33 ● b32 + a34 ● b42
c33 = a31 ● b13 + a32 ● b23 + a33 ● b33 + a34 ● b43
c34 = a31 ● b14 + a32 ● b24 + a33 ● b34 + a34 ● b44
c41 = a41 ● b11 + a42 ● b21 + a43 ● b31 + a44 ● b41
c42 = a41 ● b12 + a42 ● b22 + a43 ● b32 + a44 ● b42
c43 = a41 ● b13 + a42 ● b23 + a43 ● b33 + a44 ● b43
c44 = a41 ● b14 + a42 ● b24 + a43 ● b34 + a44 ● b44
Figure 3.1: Multiplication of matrices of size 4 4.
The two matrices A and B are shifted into the boundary processors in column 1 and row 1, respectively, as shown in Figure 3.2. The leading and trailing 0s in rows and columns are employed so that elements air and brj arrive at processor Pij simultaneously for the operation air ● brj to be performed. cij is initialized to 0 in Pij , for all i, j = 1, 2, 3, 4. At the end, processor Pij will contain cij , for 1 ≤ i, j ≤ 4
Whenever a processor Pij receives two inputs b and a from the north and the west, respectively, it performs the following set of operations, in this order:
- it calculates a ● b;
- it adds the result to the previous value cij , and stores the result in cij ;
- it sends a to Pi,j+1, unless j = 4; and
- it sends b to Pi + 1, j, unless i = 4.
This algorithm takes time O(n), for n x n matrices.
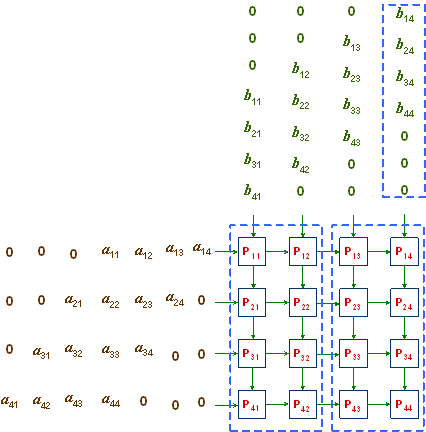
Figure 3.2: A 4 x 4 mesh (systolic array) of processors for matrix multiplication.
Experiment
Implement this parallel algorithm directly in hardware using the Altera UP 1 Education Board. Optimize your design with respect to the size of operands. Use onboard LEDs and/ or BCD displays to display intermediate and final results.
The proper operation of the entire design is to be simulated in MAX+PLUS before UP 1 is programmed. The waveforms from these simulations should be included in the lab report.