Lab 5: Operational Amplifiers; Active Filters

OBJECTIVES

Frequency response of operational amplifiers. Relation between bandwidth and gain. Slew rate. Design of first order active filters with operational amplifiers.

INTRODUCTION

Before building filters with operational amplifiers (so called active filters) we have to investigate the frequency response of a simple op-amp circuit. The circuit behaves, in fact, like a low pass filter and thus can be used as an amplifier only in a limited frequency range. There is a rule that applies to these circuits which says that the gain bandwidth product (GBP) is a constant. It means that one can trade gain for a wider frequency response. The specifications of a popular 741 op-amp give the open loop gain (no feedback) as 200,000 and the bandwidth limiting frequency of only 5 Hz (GPB = 1 MHz). From the GBP rule one may expect, for example, the bandwidth of 100 kHz with gain of 10. There are many other op-amp on the market today with larger GBP.

Frequency response is not the only characteristic that limits the speed of an amplifier. Slew rate or the maximum rate of output voltage increase is often more important in many applications which call for large signal amplitude. To understand the difference between the two consider the fact that frequency response is defined independently of the signal amplitude. If, however, the output amplitude is increased (say, by increasing the input voltage, not necessarily the gain), then the voltage has to increase faster (in V/µs) as the slope of the sinewave increases, even as its frequency does not change. Internal structure of an op-amp circuit limits this maximum slope which makes steep parts of a sine wave look like a ramp, distorting the signal. Decreasing the signal amplitude, without lowering the frequency, restores the proper waveform shape.

PRELAB

Design a first order low pass and a high pass filters using an op-amp and components available in your kit. Choose reasonable f_-3dB frequencies, from tens of Hz to tens of kHz, so that you can test these circuits with the equipment at your bench. The high pass filter should have much lower f_-3dB than the low pass filter. Simulate performance of the circuits (frequency response) with Multisim.

References:

S. Franco "Design with Operational Amplifiers and Analog Integrated Circuits", McGraw-Hill 1988. Chapter 3, especially section 3.3.

LABORATORY

Equipment needed from the stockroom: scope probe, resistance substitution box, leads.

1.      FREQUENCY RESPONSE OF A NONINVERTING AMPLIFIER AND THE GAIN BANDWIDTH PRODUCT (GBP)

Assemble a non-inverting amplifier with a low gain, up to 10. Check its frequency response. Op-amp performance is limited at high frequency; it behaves as a low-pass filter. Measure its bandwidth, which is defined by f_-3dB frequency.

Repeat the bandwidth measurements for two more resistor sets, with the amplifier gain in tens and hundreds range. Measure the gain and the bandwidth in each case.

NOTE: It is not necessary to measure a whole frequency distribution for the three cases. Measure it for the first case and then find quickly f_-3dB for the other two. A good way is to look at the phase shift between input and output signals.

2.      SLEW RATE

Measure the slew rate of the non-inverting amplifier by feeding a square wave at the input. You will get this parameter from the slope of the output waveform which will not change with increasing signal amplitude.

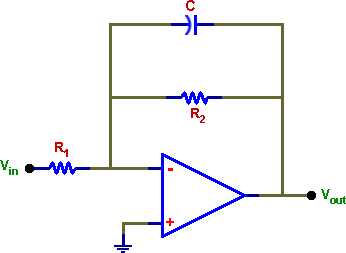
3.      LOW-PASS FILTER

Build the low-pass filter of your design and check its frequency response. Drive the circuit with a sine wave and record input (constant) and output voltage for different frequencies. Be sure to obtain more points at the "interesting" part of the curve, near and well above f_-3dB. Make preliminary graphs of the amplitude as a function of frequency in the laboratory; you will have a chance to discover early if something is wrong.

Measure also the phase shift between input and output signals. The goal is to see the phase shift as the frequency increases, passing through f_-3dB. Make the measurements also at much lower and much higher frequencies than f- 3dB. Measurement of phase shift is an accurate method of determining the filter characteristic frequency (f_-3dB).

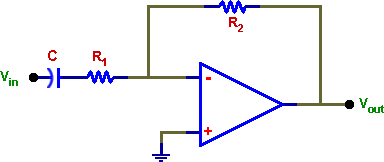
4.      HIGH-PASS FILTER

Build the high-pass filter of your design and test it like the low pass filter, above. Build the circuit on the same board but using different components. If you have more than one op-amp in the same package common power supply wiring will serve both circuits.

5.      BAND-PASS FILTER

Connect the two circuits (high-pass and low-pass filters) in series to obtain a band pass filter. (Does it matter which is first?) Verify that it performs as a band-pass filter. Alternatively, you may build a wide-band filter with a single op-amp, as shown in the figure below. For this filter to work well, the low-pass frequency (low f_-3dB) should be much lower than the high-pass (high f_-3dB) frequency.

REPORT

Besides the usual circuit information, schematics, etc. attach tables with the data on frequency response measurements (amplitude and phase). The measured frequency distributions should be presented as discrete points and the Multisim simulations as continuous curves on the same graphs. This will allow for easy comparison of the data with simulation results. See the instructions for exporting Multisim graphs to EXCEL worksheets, form which you can generate the graphs. Discuss the agreement (or lack of it) between the measured and simulated functions.